Research in Graph Theory and Network Theory: The Cable-Trench Problem
Two important problems in graph/network theory are the shortest path problem and the minimum spanning tree problem. Both of these problems have many real-world applications and there are algorithms that can find proven optimal solutions for large instances of these problems efficiently. However, Dr. Vasko, Department of Mathematics, and Dr. Ken Stott, retired Bethlehem Steel researcher, along with three Kutztown University recent graduates (at the time): Robert Barbieri (BS Math), Brian Rieksts (BS Math) and Ken Reitmeyer (BS CIS) published a research paper in the journal Computers and Operations Research in 2002 in which they define (for the first time) the Cable-Trench Problem (CTP) as a combination of the shortest path and the minimum spanning tree problems. The name "Cable-Trench" comes from the fact that a physical application of the CTP is the problem of minimizing the cost to create a campus network in which each building on a campus is connected to a central server with its own dedicated cable. There is one cost to dig trenches between buildings and a separate cost to purchase and lay the cables. In their 2002 paper, Dr. Vasko and his co-authors proved that there is no known efficient algorithm that finds the optimal solution to CTPs. Furthermore, in this paper, Dr. Vasko and his co-authors provide a comprehensive analysis of the CTP and provide an efficient approximate solution procedure for the CTP. Since the definition of the Cable-Trench Problem in their 2002 paper, other researchers from around the world have formulated important applications of the Cable-Trench Problem.
In 2011, a researcher in the Yale University School of Medicine, Dr. Yifeng Jiang, contacted Dr. Vasko informing him that he had applied the Cable-Trench Problem to develop a novel formulation for digitizing CT scan images of blood vessel networks. This, in turn, has application to medical research, cancer detection and identifying blood clots. His work resulted in very large CTPs that needed to be solved efficiently. Dr. Vasko, along with Dr. Eric Landquist, Department of Mathematics, Kutztown University, began working on the development of efficient solution procedures that generate near-optimal solutions to very large instances of the CTP and a natural generalization using actual CT scan data provided by Dr. Jiang. The research resulted in a paper that was accepted for publication in the research journal Networks in 2015, entitled "A Simple and Efficient Strategy for Solving Very Large-Scale Generalized Cable-Trench Problems" by Dr. Francis Vasko, Gregory Kresge (KU MS Computer Science), Adam Tal (KU MS Computer Science), Dr. Yifeng Jiang and Dr. Xenophon Papademetris, Yale University, and Dr. Eric Landquist.
Additionally, Mr. Ken Zyma, Kutztown University, Computer Science MS student, has written a Master's thesis on the CTP under the direction of Dr. Gregory Schaper, Kutztown University Computer Science Department and the assistance of Dr Landquist and Dr. Vasko. Mr. Zyma's thesis extends the solution approach developed by French researcher, Dr. Julien Girard in his Ph.D. dissertation on the optimal design of a collection of 96 radio telescope antenna arrays using a CTP formulation. They plan to edit Mr. Zyma's thesis for journal submission authored by Mr. Zyma, Dr. Landquist, Dr. Schaper and Dr. Vasko.
Current CTP research work by Dr. Vasko and Dr. Landquist is focused on developing efficient solution approaches for generalizations of the CTP that have important real-world applications.
The images below describe an example of the CTP. Consider a campus of nine buildings, represented by nodes 1 - 9 below such that Node 1 represents the central server. The edges between nodes represent allowable routes for digging trenches and the numbers on the edges represent the distance between buildings (in hundreds of feet, for example). See FIGURE 1.
If the trenches were free, we would want to minimize the total cable length. The bold edges in FIGURE 2 below represent the trenches that we would dig. (This is the result of running Dijkstra's Algorithm on the graph.)
If the cables were free, we would want to minimize the total trench length. The bold edges in FIGURE 3 below represent the trenches that we would dig for this scenario. (This is the result of running Prim's Algorithm on the graph.)
Suppose, instead, that it was five times as expensive to dig trenches as it was to lay cables. FIGURE 4 represents the trenches that we would dig to minimize the combined cable and trench costs.
For a problem of this size, it is relatively quick to find the minimal cost solution, but for problems involving hundreds, thousands or even millions of nodes ("buildings") that one could encounter in the real world, it is computationally difficult to find optimal solutions, so our work focuses on finding "good" solutions quickly and determining how good these solutions are.
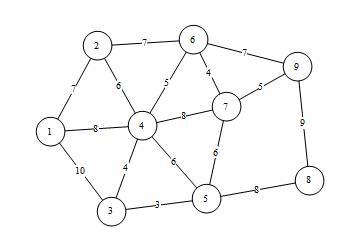
Figure 1
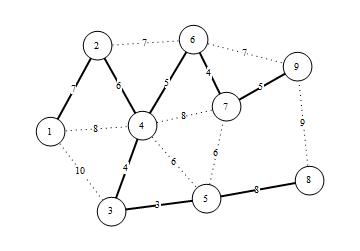
Figure 3
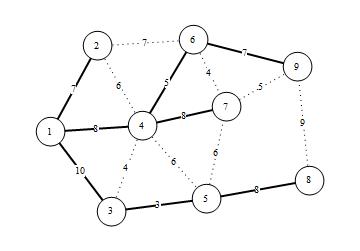
Figure 2
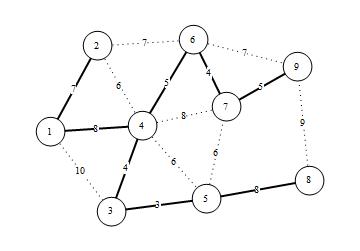
Figure 4






